fanf | Joining ellipses with matching tangents (Reply)

https://dotat.at/@/2024-02-05-joining-ellipses.html

In my previous entry I wrote about constructing a four-point egg, using curcular arcs that join where their tangents are at 45°. I wondered if I could do something similar with ellipses.

As before, I made an interactive ellipse workbench to experiment with the problem. I got something working, but I have questions...

What I wanted to do is swing a curve around a corner without cutting it. (I could solve the problem with Bézier curves, but they create other issues.) The purple ellipse in the following picture illustrates what I want to avoid: it snips off the corner of the inner rectangle.

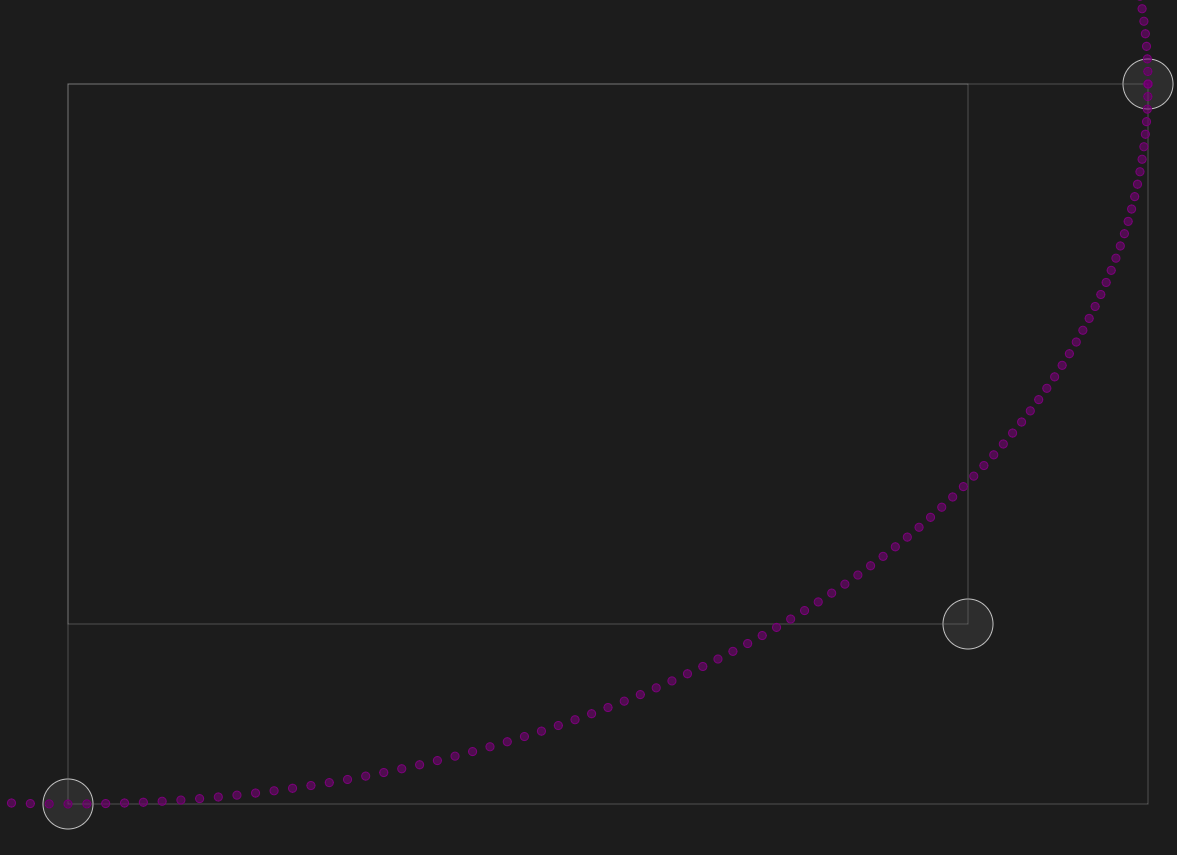
a large rectangle with a dotted purple ellipse joining oppositecorners; inside is a smaller rectangle whose corner is cut by theellipse

I managed to solve my problem by joining two ellipses so that they meet at the corner, with the constraint that (like the four-point egg) their tangents are 45°.

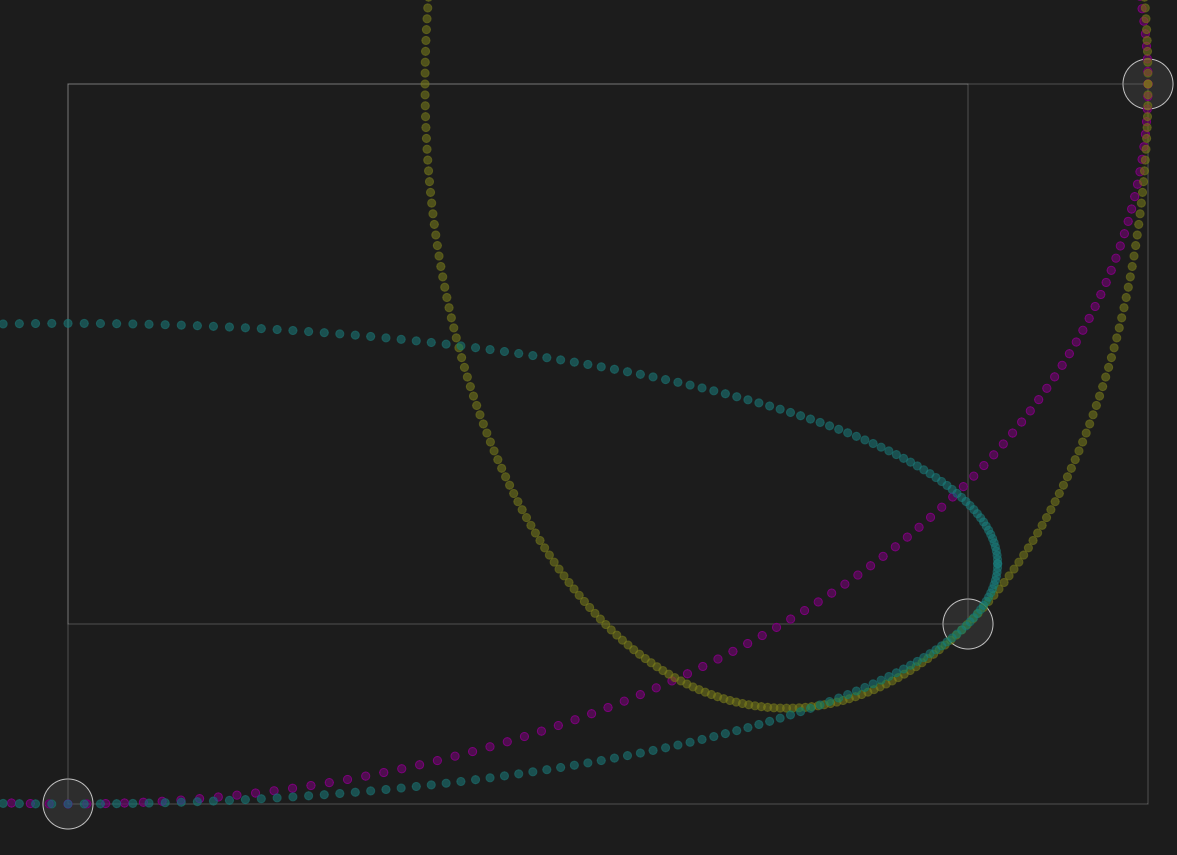
the same diagram as before, plus a yellow ellipse that matches thetangent of the purple ellipse at t he top right corner, and a blueellipse that matches the tangent of the purple ellipse at the bottomleft corner; the yellow and blue ellipses pass through the corner ofthe inner rectangle, where their tangents match

In the workbench you can drag around the big circles to see how the ellipses join.

The top right and bottom left circles control the horizontal and vertical radii of the purple ellipse. The purple ellipse isn't directly part of the solution; it's mostly for comparison.

The workbench draws a load of extra scaffolding lines. The lines joining at the corner of the inner rectangle show that the tangents and normals are 45°.

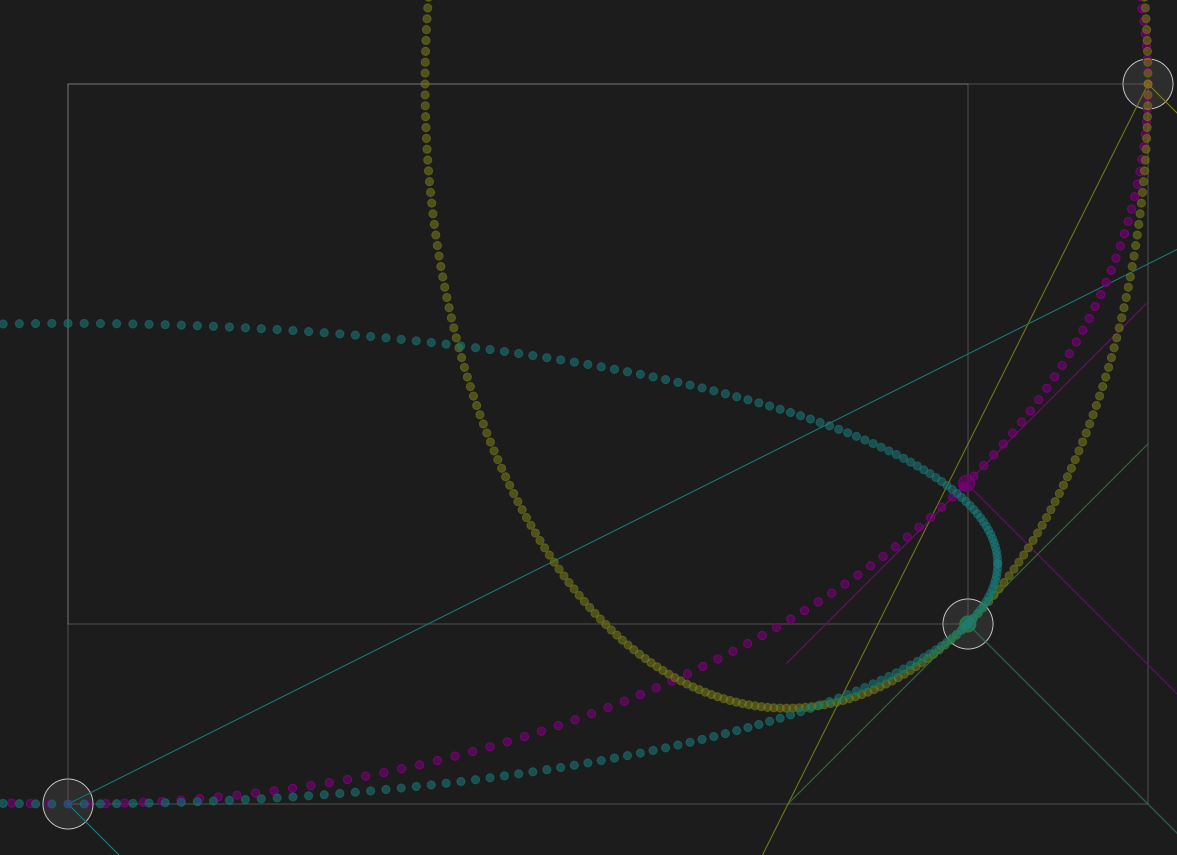
The lines joining the top right and bottom left circles are my eyeballed guesstimates of the region in which a solution can be found.

the same diagram as before, with extra lines showing where thetangents and normals of the ellipses are 45°, and the boudariesoutside which there is no solution

questions

Is there a formula?

I tried to work out how to directly calculate the radii of the solution ellipses. I thought I had something plausible based on a parametric ellipse using the tangent as the parameter, but it didn't work when I tried it out.

In reaction to that failure, I made the workbench to try to get a better intuition of what is going on. Eventually I tried bodging it with a brute-force search for a solution. This worked better than expected.
Why does a simple iteration converge so nicely?

The search isn't really a search as such:
1. start off with the purple ellipse
2. find the point where its tangent is 45°
3. take the X and Y distances from the target point
4. subtract the distances from the ellipse's radii
5. repeat until converged
I was surprised that this does in fact converge, and does so rapidly. I didn't even have to break out Newton-Raphson or quadtrees! Accidentally logarithmic?
What are the constraints on a solution?

The workbench draws lines with gradient 1/2 radiating from the top right and bottom left corners. The two lines pointing inside the rectangle are empirically a fairly accurate match for the boundary between possible and impossible solutions.

I am surprised these are simple straight lines, not curves.

It's even possible to solve if you drag the corner outside the rectangle, though the ellipses make interesting cusps if you do that. However my eyeballed guesstimate at the outer boundary lines is not accurate.